2023年度の大阪公立大学の化学の分析と来年度に向けた対策、問題の解答解説を載せたいと思います。
2023年度大阪公立大化学の分析
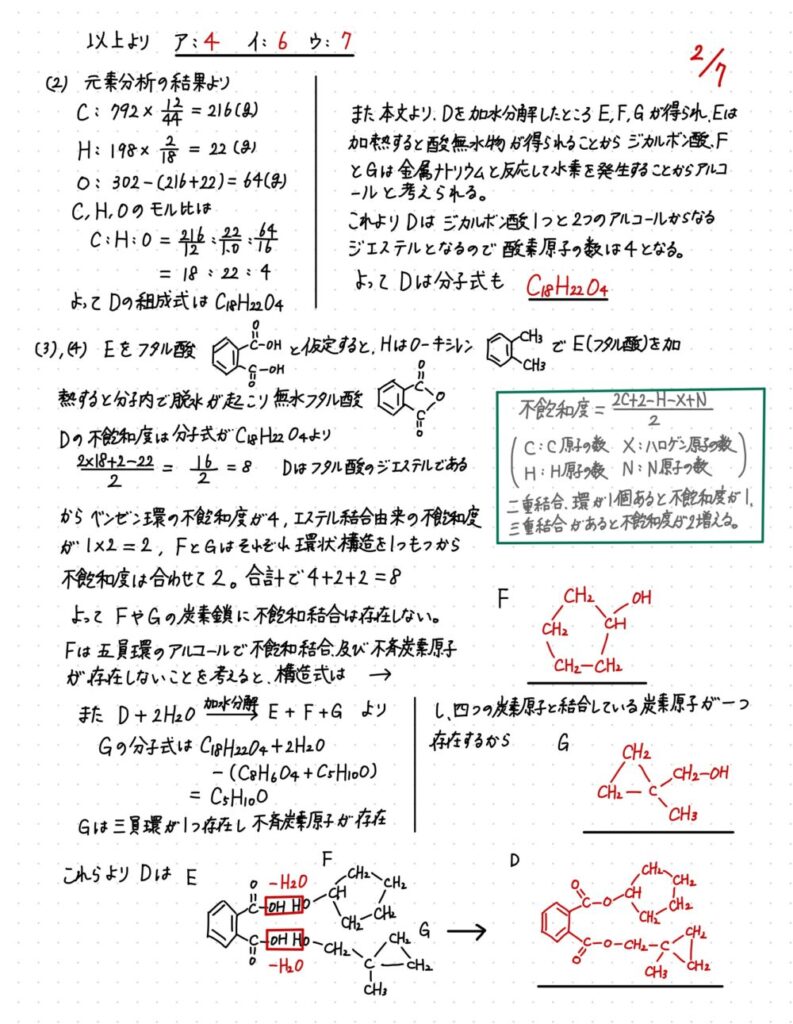
第1問 C5H12(ペンタン)の誘導体、フタル酸ジエステルの構造決定
C5H12(ペンタン)の構造異性体とその水素原子の1つまたは2つをヒドロキシ基で置換した異性体を正確に書く必要がある。本文中の、各アルコール中の一つの炭素に複数のヒドロキシ基が結合していないものとし、鏡像異性体の数は含まれないものとするに注意しよう。
元素分析は化合物Dの組成式がまず整数値でC18H22O4と求まり、それ以降の文章からDがフタル酸のジエステルと決定できれば分子式もC18H22O4と容易に求まる。ヨードホルム反応により生じる化合物Iも差がつくポイントなのでよく整理しておこう。
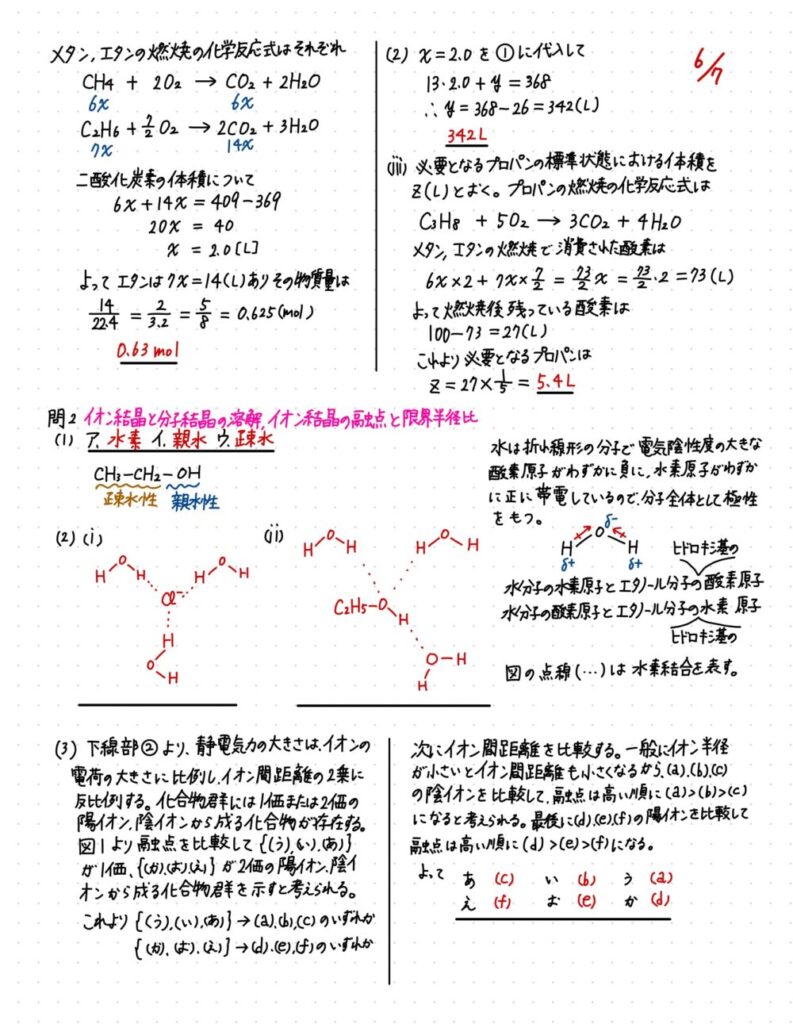
第2問 問1 化合物の電子式・分子の形状と極性、シュウ酸カルシウム水和物の熱分解
問2 硫化カドミウムの溶解平衡・溶解度積
問1 前半は、各原子の原子価とオクテット則を基に電子式を書けばよい。BF4−(テトラフルオロホウ酸イオン)は初めて見た人も多いと思うが、四塩化炭素(CCl4)を思い出して推測しよう。
後半は、今までこの大学では出題されなかったラスボス級の問題である。シュウ酸カルシウム一水和物・ニ水和物の混合物の加熱で両方ともシュウ酸無水物に変化することが分かれば、2つの未知数x、yを条件に当てはめて連立方程式を解けばよい。
問2 (2)で手が止まった人が多いかもしれない。本文からm=〔S2−〕+〔HS−〕+〔H2S〕の関係に気づけば解き進めていける。溶解度積Kspは飽和溶液の陽イオンと陰イオンの濃度の積であることを確認しておこう。
第3問 問1 同位体と原子量、混合気体の燃焼と体積
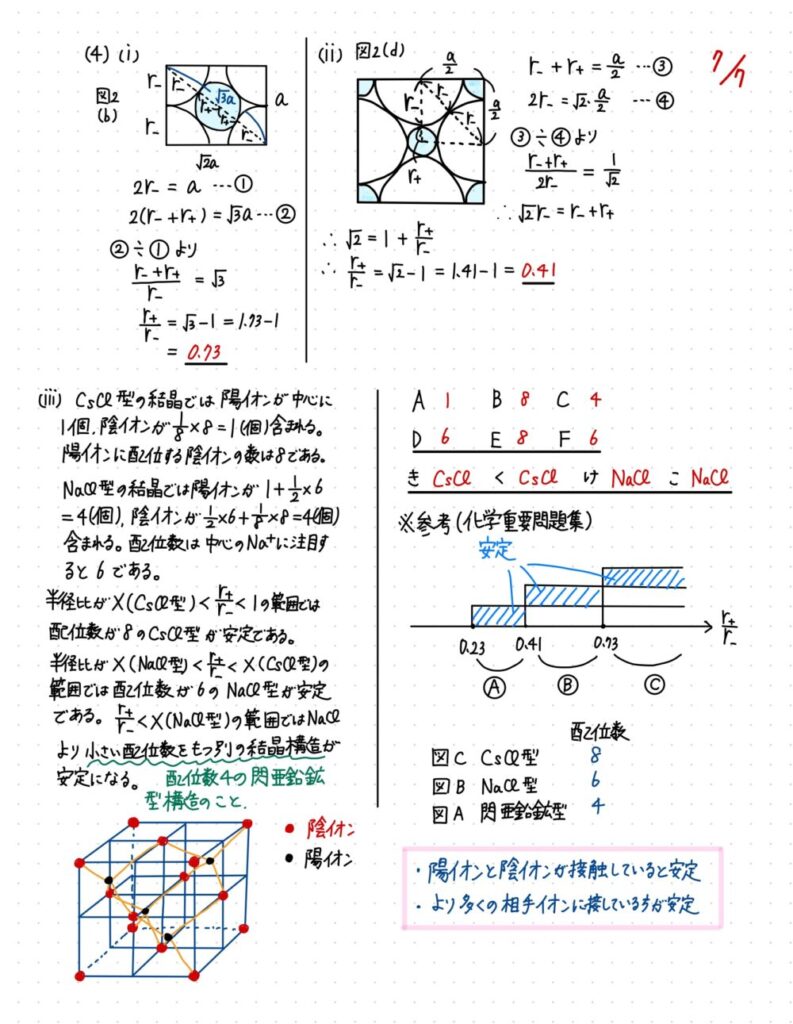
問2 イオン結晶と分子結晶の水への溶解、イオン結晶の限界半径比
問1 基本的な問題である。前半の(4)では袋から球を取り出す場合の数の考え方をイメージして、存在比を掛け合わせた後、2倍することを忘れないようにしよう。後半は同音・同圧の体積比=化学反応式の係数比を思い出して、反応前・変化量・燃焼後のバランスシートを書いて解き進めば正しい答えが得られる。
問2 前半の(1)、(2)はそのまま水和の話で基本的である。(3)の融点と結晶中のイオン間距離の問題では、イオンの電荷とイオン間距離に注意して本文中に書いてあるヒントを参考にすれば解き進めていける。後半の(4)は限界半径比でラスボス級の問題である。とは言え、最もオーソドックスな形で出題されているので、この内容を定着させていた受験生は有利だっただろう。
来年度に向けた対策
教科書とセミナー化学やリードαなどの教科傍用問題集で一通り単元別の学習を仕上げた後、重要問題集のA問題と必要なB問題に取り組もう。実験操作や方法などについてもよく出題されるのでサイエンスビュー化学総合資料集のような資料集を用いて、ビジュアル的にも内容を深く定着させておきたい。さらに余裕があれば、化学の新演習を用いて大阪公立大学で出題されそうなラスボス級の問題を想定して万全の対策をしておくとよい。
2023年度大阪公立大(前)化学の解答解説







コメント